Week 2 – Boolean Logic

Boolean Logic

What are we covering:

computer>> CPU >> ARITHMETIC AND LOGIC UNIT >> TRUTH TABLES >> BOOLEAN LOGIC >> LOGIC CIRCUITS

 

---

Laws of boolean logic:

Name	AND form	OR form
1.       Identity	1x = x	0 + x = x
2.       Null	0x = x	1 + x = 1
3.       Idempotent	xx = x	x + x = x
4.       Inverse	x x` = 0	x + x` = 1
5.       Commutative	xy = yx	x + y = y + x
6.       Distributive	(x + y)z = xz + yz	(xy) + z
7.       Absorption	x + (x +y) = x	x + (xy) = x
8.       De Morgan’s	(xy)` = x` + y`	(x + y)` = x`y`

NOTE: (xy)` does not equal to x`y`

---

Application

We use boolean logic to make claims and put sentences into logic forms . Let us start off with an example to see what I’m talking about and how it works

Given: it’s not safe to go outside during full moon and during the night of full moon

let x be true if it’s night and let y be true if it’s full moon

List all the outputs in boolean logic form that indicate it’s safe to go outside, given that its not safe to go outside during full moon and during the night of full moon

Answer: It’s safe to go outside when –>    not x and not y – (x + y);       x and not y – (x ^ y);

---

Boolean simplification

• Why do we perform the simplification? — the answer to that is we want to reduce the number of gates  to keep it easy and clear. More gates are more costly, more power consuming etc.

Example 1:

Simplify this expression: f (x,y,z) = x ‘y z + x’ y z’  + xz

Let us use basic algebraic method for performing the first step, x’ y ( z + z’) + xz

By the inverse rule we know that z + z = 1, hence 1x’y + xz

There is no way to simplify it further, hence we are done here.

Example 2:

Prove that (x + y)(x’ + y) = y

We could prove it by the truth table when asked to, but it’s more time consuming with the truth table than it is by the boolean logic simplification.

Truth Table Approach:

x	y	x`	(x v y)	(x` v  y)	(x v y) ^ (x`v y)
T	T	F	T	T	T
T	F	F	T	F	F
F	T	T	T	T	T
F	F	T	F	T	F

Boolean Logic Simplification Approach:

Prove (x + y)(x’ + y) = y

= xx’ + x’y +xy + yy

=0 + x’y + xy + 0

= xy + xy

= y( x + x)

=y proven

Example 3:

( A + B) (A + B) B

=(A+B)(AB + BB)

= by the inverse rule b b = 0, so we have (A+B)(AB + 0)

= by identity rule AB + 0 = AB, so we have (A+B)(AB)

= AAB + ABB

= 0B + 0A

=0

Example 4

Example 5

solved using XOR and De Morgan’s Law mainly

 

 

 

 

 

 

 

 

 

 

 

 

 

Example 6:

[UNDER- CONSTRUCTION]

---

Drawing circuit using the simplified boolean logic function

 Example 1

Create the circuit for (x + y)(x + y)

Notice there are two OR logic expressions in the brackets and they together are tied to each other by the AND logic gate. Here’s how you represent their circuit:

---

Get the Boolean Equation – Performing Reverse Operation 

Example 2:

Perform a reverse operation. You are given a circuit of boolean logic gates, get the equation by analysing the circuit and give the equations simplest form

 

((xy)’ +(xy)’) + (z + y)

simplification:

By De Morgan’s  law = ((x + y) + (x + y)) + (y + z )

By the inverse rule and idempotent rule = (x + y + x + y) + (y + z)

By Null property = (x + 1) + y + z

By Null property = 1 + y + z

=1

---

Creating circuits from truth tables using Disjunction Normal Form DNF

We already know that circuits can be created from boolean logic equations and we’ve seen how just above. But did you know that circuits can also be created using truth table? Yes, it’s true we may be given a truth table and asked to draw its circuit. How we complete this we first convert our truth table into boolean logic equation known as disjunction normal form (DNF), and using DNF we may easily create our circuit.

Let’s do an example to clarify it all.

Example

Given a truth table, draw its circuit

x	y	z	Output
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	0
1	1	1	1

 Step 1: From the table above, create a smaller table of output 1 only.

x	y	z	Output
0	0	0	1
0	1	0	1
0	1	1	1
1	0	0	1

Step 2: For each of the output above write the corresponding boolean logic function which is in the DNF form

not “a” will be marked like this –> a’

For instance we have x=0, y=0 and z=0 as our first line of the table. The zero represents false/not. So here’s how we may write it –>>  x’y’z’ (meaning x not and y not  and z not). Now write all the other equations accordingly and combine them with the “+” sign.

f(x,y,z) = (x`y`z`) + (x`y`z`) + (x`y z`) + (x`y z) + (x y`z`) + (x y z )

Step 3: Create its circuit.

Notice all of these expressions in the brackets are connecting to one another with a plus sign, and we already know that the + sign in boolean logic means OR,therefore we now know all the expressions in the bracket are connected to one another by the OR gate and since they are being multiplied to each other inside the bracket this means that they’re connected to one another via AND gate. Hence our picture should consist of 6 AND logic gates connected to each other by the OR gate. This is what we come up with:

 

Exercise:

Create the circuit by the given truth table & don’t look at the answer until you have fully completed or at least attempted it:

x	y	z	Output
0	0	0	0
0	0	1	1
0	1	0	0
0	1	1	1
1	0	0	1
1	0	1	0
1	1	0	1
1	1	1	1

Answer:

x	y	z	Output
0	0	1	1
0	1	1	1
1	1	0	1
1	0	0	1
1	1	1	1

 

---

NAND GATE

• NAND gate tends to be the universal gate in logic gates, what that means is that we could represent any gate using the NAND logic gate whether that’s the NOT gate, the AND gate or the OR gate.
• It will not make much sense until it’s witnessed and proven by both the circuit and by De Morgan’s rule
• The reason why we are encouraged to know NAND gate is to be able to construct other gates with the help NAND and the inverters (NOT gate) only. This is due to the CMOS technology which is highly popular today.
• CMOS technology only understands negation or in other words the circuits constructed of NANDS, NOTs and NORs and since almost everything could be presented by the NAND gate we do not bother using other gates sometimes.
• CMOS technology is used in microprocessors, microcontrollers, static RAM, and other digital logic circuits
• It’s sometimes easier to solve the boolean logic equation first in order to easy built the its corresponding circuit.

Representation & Equation for NOT GATE using NAND gate

let x` be -not x

Have a look at this:

(xx)` = x` + x’ (by De Morgan’s Rule) = x` (Idempotent rule)

Notice, we have passed two x’s into the NAND gate- what this means this means that they are being multiplied to each other first (xx) and the negation of NAND is only applied afterwards. Hence the negation sign is over the bracket as shown in the equation above. If you follow the equation carefully and understand its simplification you will know that indeed we obtain the objected output of x` using the NAND gate.

Representation and Equation of the AND gate using the NAND gate

let a` represent – not a

Step 1: pass a  and b into the NAND gate = (ab)`

Step 2: connect (ab)` to itself and pass it into another NAND gate = ((ab)'(ab)`)’ = ((ab)`)` + ((ab)`)` = ab + ab = ab

In the diagram above we have connected A and B using the NAND gate first. We get (AB)` out of that first NAND gate and we connect it to another (AB)` or in other words another one of itself and pass this to the second NAND gat, by doing that we obtain the AND gate output of AB. The equation above suggests the same. Hence we were able to achieve the AND output using the NAND gate.

Representation and Equation of an OR GATE using the NAND gate

Step 1: pass x and itself into a NAND gate to create a x not

Step 2: pass y and itself into a NAND gate to create a y not

Step 3: connect x` and y` via a NAND gate

(x`y`)` = (x`)` +  (y`)` (De Morgan’s Law) = x + y (double negation cancels the negation)

 

 

---

Converting DNF equations into circuit of nand gates

We are now capable to deriving the DNF equation out of any truth table. We are also capable of then drawing a circuit by the DNF equation obtained, but that only limits us to one way of presenting that circuit and trust me that is not the ONLY way to do it. We’ve just talked about the universal gate NAND which is able to represent any Logic gate, this means that we are indeed able to represent our circuit with the use of NAND gates only and that’s the other possibility of drawing it. So how do we do that?

EXAMPLE

W	X	Y	Z	Output
0	0	0	0	0
0	0	0	1	1
0	0	1	0	1
0	0	1	1	1
0	1	0	0	0
0	1	0	1	1
0	1	1	0	0
0	1	1	1	1
1	0	0	0	0
1	0	0	1	0
1	0	1	0	0
1	0	1	1	1
1	1	0	0	0
1	1	0	1	1
1	1	1	0	0
1	1	1	1	0

Deriving the DNF equation out of the table:

w	x	y	z	Output
0	0	0	1	1
0	0	1	1	1
0	0	1	0	1
0	1	0	1	1
0	1	1	1	1
1	0	1	1	1
1	1	0	1	1

f(w,x,y,z) = W`X`Y`Z  + W`X`Y Z + W`X`Y Z` +  W’ X Y’ Z + W’ X Y Z + W X `Y Z + W X `YZ  

DRAW IT USING THE NAND GATE:

You must be wondering, why I have we put the negations correctly since it’s going to be negated/reversed anyway by the NAND gate which wxyz are connecting to. Well here’s the thing: first of all you must put the negations where they are supposed to be, and now don’t ignore the next NAND gate which is connected all the smaller NAND gates. I suggest you solve this equation by hand to understand what’s going on, but the answer will still be given below just in case you fail to solve your equation.

 Answer:

f(w,x,y,z) = W`X`Y`Z  + W`X`Y Z + W`X`Y Z` +  W’ X Y’ Z + W’ X Y Z + W X `Y Z + W X `YZ

let’s use the first two expressions of the DNF equation above for explanation purpose only:

f(w,x,y,z) = W`X`Y`Z  + W`X`Y Z

now we apply the effect of NAND on them separately first and them on their combined result as the circuit diagram suggests:

You must already know that we multiply the variable when are connecting to each other via the  AND or NAND gate. So here’s what our equation looks like:

((W`X`Y`Z)`(W`X`Y Z)` )`

let a= W`X`Y`Z  and b= W`X`YZ

So we have (a`b`)` = (a`)`+ (b`)` (by De Morgan’s law) = a + b (as double negation cancels  the negative effect)

and hence we’ve achieved what we wanted, now if we change a  and b back to their origin values we get what we had started with, hence the circuit diagram is correct. However if the second NAND gate was being used then we don’t quite achieve what we wanted and had to use the inverter (NOT GATE made using the NAND gate)

---

MULTIPLEXER – MUX

• Used for selection purposes
• Used for selecting one input as the output from multiple inputs inserted
• There exists a 4:1 multiplexer and a 8:1
• The control wires are based on [under construction]
• Here is how it looks:

For a regular table of three variables x,y,z we use the 8:1 multiplexer normally as it generates 8 inputs and each goes in separately.. However we could implement the same function of three variables x,y,z using 2 controllers and 4 inputs by the 4:1 multiplexer. The question is how?

Procedure:

Step 1: Get the DNF form from the truth table

Step 2: Once the DNF form of the function is obtained, select any two variables as control lines and the output will be derived in terms of the third non-selected variable in step 3

Step 3: Create a residual table using the two selected variables. The example will help you understand

Example:

Given: The truth Table and the function in DNF form f(x,y,z) = x`yz` + x`yz

x	y	z	f (x,y,z)
0	0	0	0
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	0
1	1	1	0

Variables chosen: x and y

Now derive the residual values of x and y in term of z, how do we do that?

Take all the different values of x and y in order construct the residual table. When x = 0 and y = 0 in the truth table above we have two different vales for z but the same value for the output f(x,y,z). We must only consider the output where f(x,y,z) = 1, since there is none in this case, we claim that the residual is 0.

Now let us take other values of x and y:  x = 0 and y = 1. Even though z has two different output values in this situation, we consider the line that generate the final output 1. In this case since the output tends to be 1 in both case we shall consider both these cases. This is what goes into the residual table: values of z encountered were 0 and 1 and when we add not z to z we end up with a one.

For (x = 1 and y = 0) and for (x=1 and y=1) the output does not equal 1 regardless of z. Hence the residual becomes zero.

x	y	Residual
0	0	0
0	1	z` +  z = 1
1	0	0
1	1	0

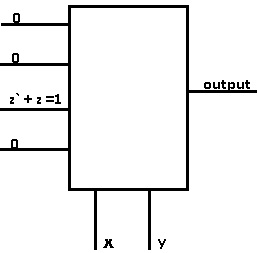
Here’s how your output for the truth table above can be represented, using the 4:1 MUX:

Exercise

Now with x and z as variables/control lines, draw the residual table and DO NOT LOOK AT THE ANSWER BELOW

Answer:

x	z	residual
0	0	y
0	1	y
1	0	0
1	1	0

exercise 2

Given the truth table – construct a residual table and draw its 4:1 MUX diagram:

x	y	z	F(x,y,z)
0	0	0	1
0	0	1	0
0	1	0	1
0	1	1	1
1	0	0	0
1	0	1	0
1	1	0	1
1	1	1	1

Answer:

y	z	Residual
0	0	x`
0	1	0
1	0	1
1	1	1